Aim:
To determine the metacentric height of a flat bottomed pontoon.
Experimental setup:
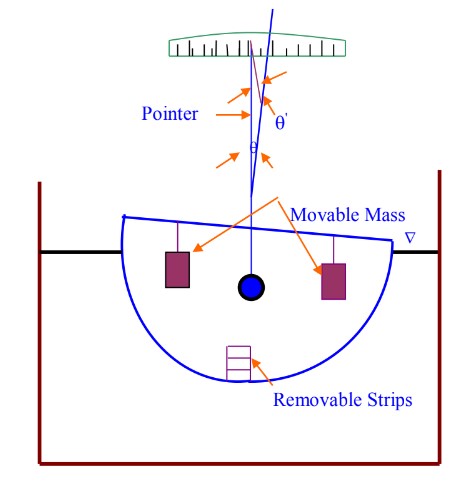
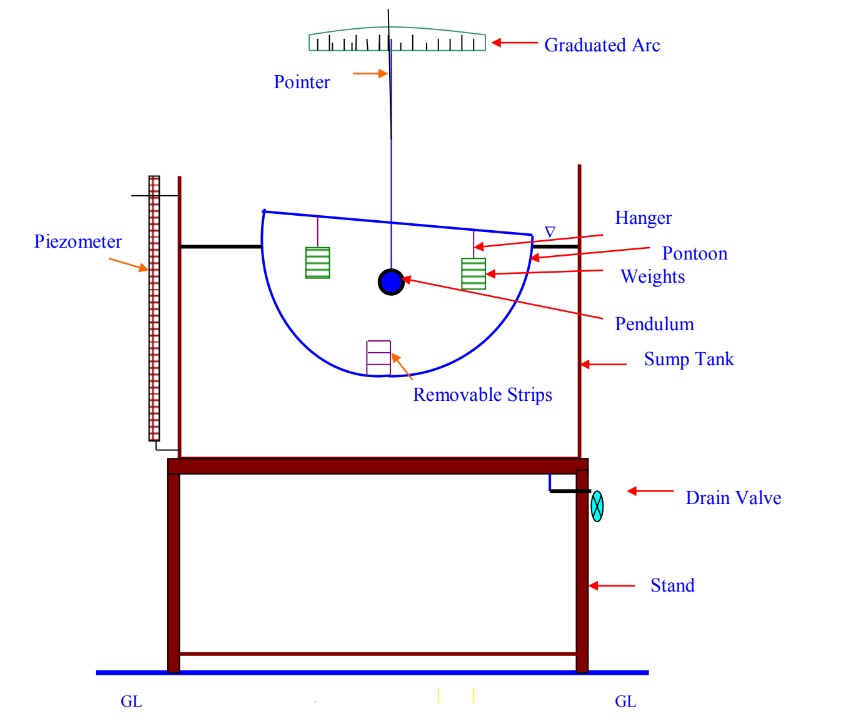
The experimental set up consists of a pontoon (flat bottomed vessel), which is allowed to float in a M.S tank having a transparent side. Removable steel strips are placed in the model for the purpose of changing the weight of the vessel. By means of a pendulum, the angle of tilt θ can be measured no a graduated arc. For tilting the ship model, a crossbar with two movable hangers is fixed on the model. Pendulum and graduated arc are suitably fixed at the centre of the cross bar.
Formulae:
Metacentric height, `GM = \frac{w_{2}x}{W\tan\theta}` cm
where,
w2 = Weight placed on pontoon in gms (remains constant in constant weight method)
x = Distance of unbalanced mass from the center of the crossbar in cm (remains constant in constant distance method)
θ = Angle through which pontoon is tilted in degrees
W = Weight of pontoon along with the unbalanced mass in gms = w1 + w2
w1 = Weight of pontoon in gms = HAρ
A = Cross sectional area of the tank in cm2
ρ = Density of water = 1 kg/cc
H = Difference in level of water in the tank after pontoon is placed in cm = H2 - H1
H1 = Initial level of water in tank without pontoon in cm
H2 = Final level of water in the tank with pontoon in cm
Theory:
A body floating in a fluid is subjected to the following system of forces:
1. The downward force of gravity acting on each particle that goes to make up the weight of body, Wc acting through centre of gravity G.
2. The upward buoyant force of the fluid acting on the various elements of the submerged surface of the floating body FB, acting through centre of buoyancy B.
For a body to be in equilibrium on the liquid surface, the two forces Wc and FB must lie in the same vertical line i.e. these two forces must be collinear, equal and opposite.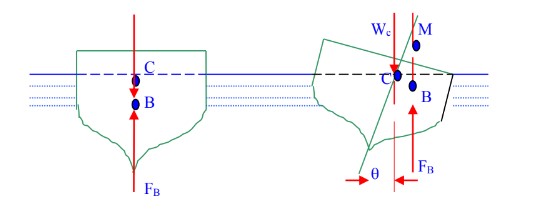
When the vessel has been tilted through an angle , the centre of gravity C of the body G, is usually remains unchanged in its position, but B i.e. centre of buoyancy will generally change its position, thus Wc and FB forms a couple. The line of action of FB in the new position cuts the axis of the body at M, which is called the metacentre and the distance CM is called the metacentric height. The metacentric height is a measure of the static stability of the floating bodies.
The metacentric height can be obtained by equating righting couple and applied moment,
` = \frac{W_{c}X_{d}}{(W_{c}+W_{m})\tan\theta}`
where,
Wc is the weight of vessel
Wm is the weight of unbalanced mass causing moment
on the body
Xd is the distance of the unbalanced mass from the centre of the cross bar.
Procedure:
1. Note down the relevent dimensions as area of collecting tank, mass density of water etc.
2. Note down the water level in the tank when pontoon is not in the tank.
3. Pontoon is allowed to float in the tank. Note down the reading of water level in the tank. Mass of pontoon can be obtained by the help of Archmidie's principle.
4. Position of unbalanced mass, weight of unbalanced mass and the angle of heel can be noted down. Calculated the metacentric height of the pontoon.
5. The procedure is repeated for other positions and value of unbalanced mass.
6. Also the above procedure is repeated while changing the weight of the pontoon by changing the number of strips in the pontoon.
Observations:
Area of the tank, A = .......... cm2
Table:
| SNo. |
H1 (cm) |
H2 (cm) |
H (cm) |
w1 (gms) |
x (cm) |
θ (°) |
w2 (gms) |
w (gms) |
GM (cm) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 |
Graphs:
Graph is plotted between: (for both constant weight and constant distance method)
1. GM Vs tanθ
Precautions:
1. Apparatus should be in levelled condition.
2. Reading must be taken in steady condition of water.
3. Unbalanced mass should be measured by taking care that water disturbance should be minimum.
4. Reading of tilt is to be taken when the pendulum becomes steady and does not fluctuate.
Result:
a) Average metacentric height of pontoon from constant distance method = .......... cm
b) Average metacentric height of pontoon from constant weight method = .......... cm